| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 초보영어
- 영어
- 3dprinter
- machinevision
- 파이썬gui
- 인공지능
- Python
- 영어기초
- Ai
- opencv
- 산업대학원
- ComputerVision
- 영어회화
- 4차산업
- coding
- 대학원
- 머신러닝
- 동사
- 특수대학원
- 프로그래밍
- 영어공부
- Vision
- 딥러닝
- 석사
- 직장인
- 코딩
- 파이썬
- 오픽
- 머신비전
- C언어
- Today
- Total
미래기술연구소
LQR 제어 란 ? 본문
□ LQR(Linear quadratic regulator)
특정한 양을 performance measure로 잡아주고 이를 최소화하는 컨트롤러를 설계하는 것.
흔히 최적제어론(optimal control)이라고도 하는데 이는 위에서 구한 컨트롤러가 performance measure를 최소화 시켜주기 때문이다.
• Linear: 선형이라서.
• Quadratic: performance measure는 계산을 간단하게 하기 위해 대개 제곱 꼴로 잡기 때문에 들어가는 수식어.
• regulator: 제어에서는 무언가를 줄여주는 행위를 regulate라고 한다. (에러, 불필요한 진동 등.)
LQR 제어는
1)시스템의 상태방정식 구하고
2)퍼포먼스 메져 정하고
3)리카티 미방 풀면 끝이다.
※ LQR과 칼만 필터랑 합친 것을 LQG(linear quadratic Gaussian)라고 한다. 칼만필터가 가우시안 분포를 써먹기 때문에 이런 이름이 붙었다. LQG에서는 칼만필터를 사용하기 때문에 유한시간 LQR은 못 써먹고 무조건 무한시간 LQR 밖에 안 된다.(리카티 이퀘의 솔루션이 상수가 되기 때문.)
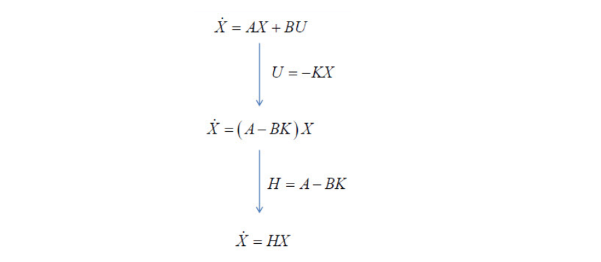
일반적인 선형시스템의 상태방정식은 dot_X = A*X+B*U의 형태입니다. 거기서 제어입력 U를 U=-KX 로 두고 다시 정리하면 dot_X=(A-B*K)*X 가 되는데요. 이걸 다시 H=A-BK로 두고 위와 같이 정리해둘 수 있습니다.
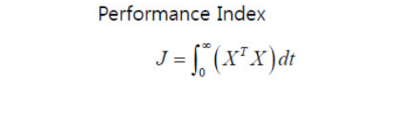
일단 성능지표(performance index)라고 하는 것을 위와 같이 생각해 볼 수 있습니다. 위의 상태 X는 벡터의 형태이기 때문에 사실상은 각 상태의 제곱의 합으로 표현한 것입니다. 상태의 제곱의 합이 작을 수록 좋은 것이지요. 결국 위의 정능지표를 최소화하는 뭔가가 필요한 것입니다.

이제 다시 일반적인 시스템에서 위의 수식을 만족하면 시스템은 안정(stable)하다고 볼 수 있습니다. 그러면, 그렇게 만들어주는 행렬 P를 찾으면 되는 것이지요.
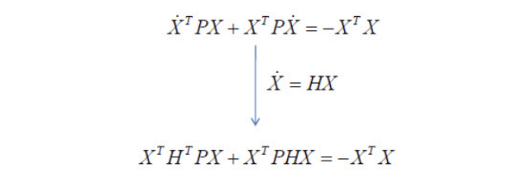
그것을 대입해서 정리하면 됩니다. 그러면 위의 마지막 수식에서
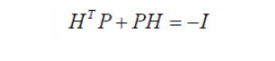
이걸 만족하는 P,H를 찾으면 되죠. 문제는 식하나에 미지수가 2개네요.

처음 생각했던 성능지표에 다시 대입해서 풀면
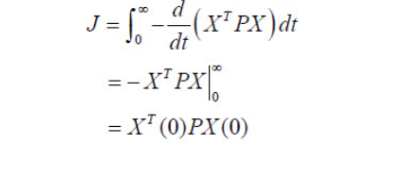
를 찾을 수 있습니다. 이제
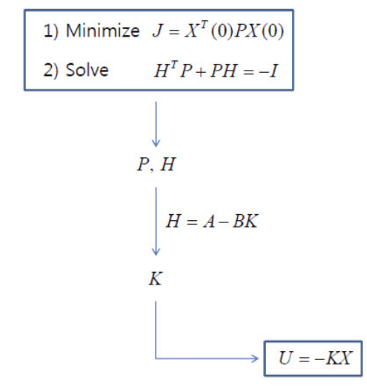
위의 1,2번 식을 만족하는 미지수 P,H를 찾으면, 제어게인 K를 찾을 수 있습니다. 그런데 일반적으로 성능지표는 각 상태에 가중치를 줄 수 있고, 제어입력의 크기에 대해서도 가중치를 설정할 수 있도록
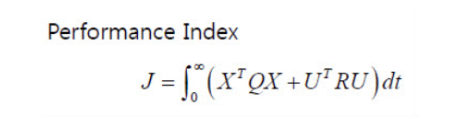
를 많이 사용하는 편입니다. 문제는 성능지표를 MATLAB을 이용하여 풀면
MATLAB 이용한 LQR 게인 구하기
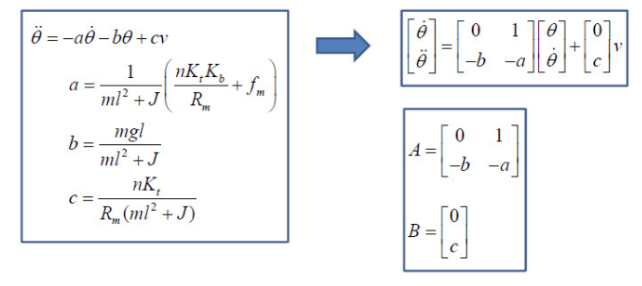
지난 시간까지 우리가 다루던 시스템의 상태방정식입니다. 여기서 A, B행렬을 얻을 수 있다.

그리고, Q, R을 적절히 선정하고 MATLAB에서 LQR이라는 명령을 사용해주면 된다.
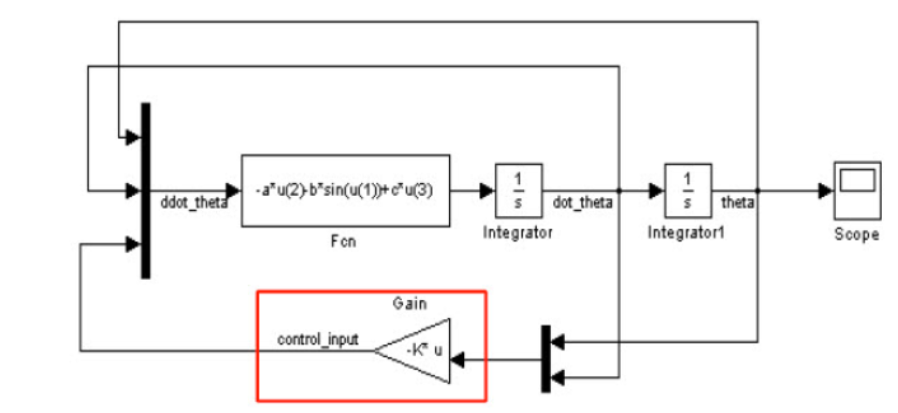
위 그림은 시뮬링크에서 LQR게인을 적용한 부분입니다.
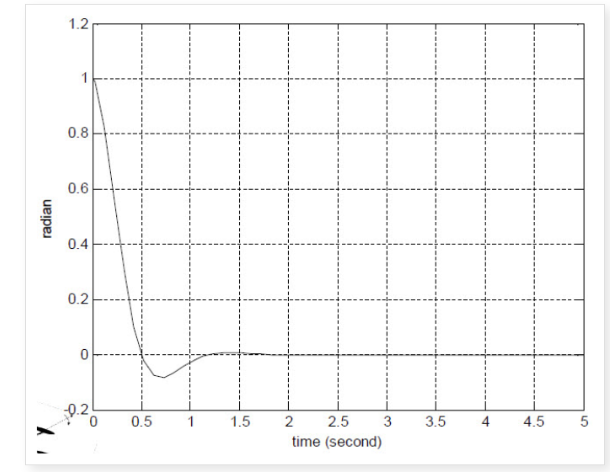
여기서 Q, R값을 조절해 보면 좀 더 성능이 좋아 질 것이다.
□ LQG(Linear Quadratic Gaussian)
LQ optimal control을 통해 구한 control gain과 Kalman filter를 이용하여 estimated state를 구하는 방법. 이는 Stochastic optimal control이라 부르기도 합니다. State space 모델에 LQ optimal control과 Kalman filter를 모두 표현하면 식 1과 같이 나타낼 수 있습니다.
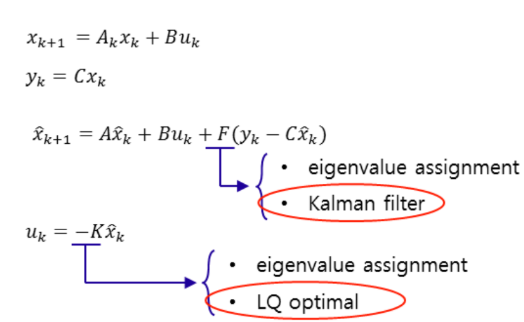
식 1을 정리하면 식 2와 같이 나타낼 수 있습니다.
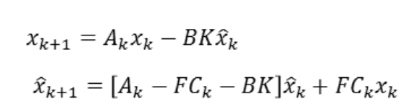
식 2를 다음과 같이 새로운 state를 선언하고 식 3과 같은 관계식을 만들 수 있습니다.
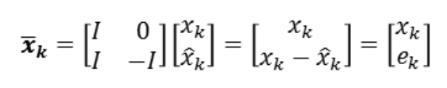
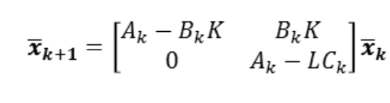
식 5를 통해 error와 state는 독립적이며, LQ optimal control gain을 구하는 과정과 Kalman gain을 구하는 과정이 독립적이라는 것을 알 수 있습니다. 식 5의 eigenvalue는 식 6과 같이 나타낼 수 있습니다.
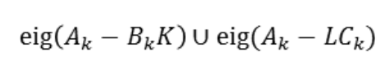
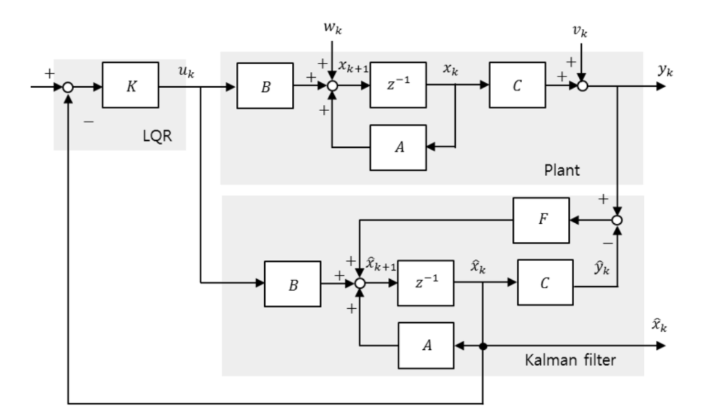
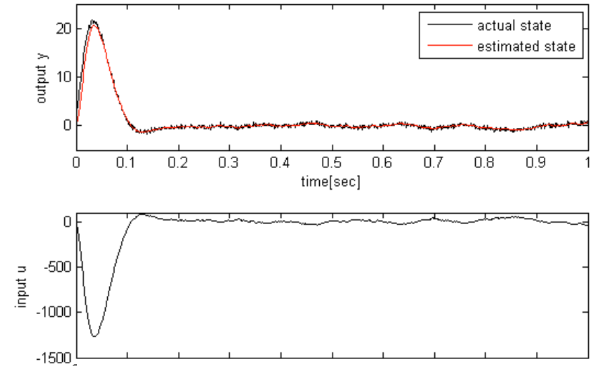
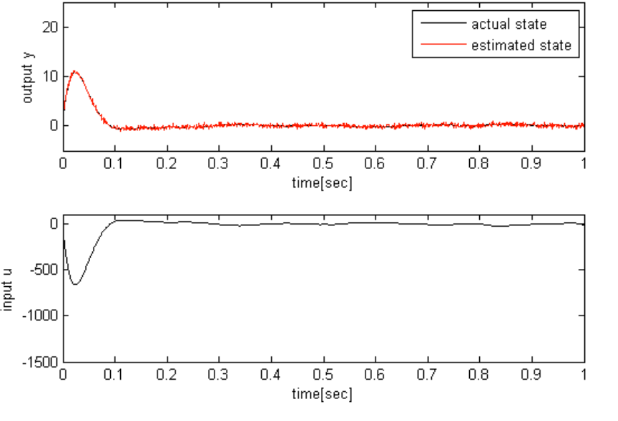
위의 코드를 통해 eigenvalue assignment과 Kalman filter를 이용한 observer의 제어 성능 차이를 보고자 합니다. 그림 2는 LQ optimal control과 eigenvalue assignment를 통한 observer, 그림 3은 LQ optimal control과 Kalman filter를 통한 observer입니다. 그림 2는 그림 3보다 state를 늦게 예측함과 더불어 입력 u도 크고 0으로 수렴하는 응답속도도 느립니다. Kalman filter를 통해 노이즈를 통계학적으로 고려한 결과 state를 정확하게 예측할 수 있고 정확하게 예측한 state를 통해 LQ optimal control을 하기 때문에 작은 입력으로 더 빠르게 수렴하는 것을 확인할 수 있습니다.
'Industry 4.0 > Control Engineering' 카테고리의 다른 글
| State feedback control (0) | 2020.06.22 |
|---|---|
| Linear systems (0) | 2020.06.22 |
| Kalman Filter (0) | 2020.06.01 |
| Kalman filter란? (0) | 2020.06.01 |
| 제어공학 강의자료 (0) | 2020.05.10 |




