Linear and Logistic Regression

선형 회귀와 로지스틱 회귀는 가장 기본적인 기계학습 기법입니다.
선형 회귀 (Linear Regression)
선형 회귀는 선형의 데이터가 들어왔을 때, 어떤 투입 값이 들어오면 그 투입 값에 해당하는 산출 값을 예상하는 태스크입니다. 먼저, 모델이라고 볼 수 있는 가설 (Hypothesis)를 세웁니다. 선형 회귀의 경우는 가설이 선형식으로 이루어집니다. 일변수 일차원 선형 회귀를 생각해보겠습니다. 투입 값을 x, 산출 값을 y라고 하면 가설 H(x)는 다음과 같습니다.
통계학적으로 적절한 W, b를 추정하는 방식이 있지만 기계학습에서는 ‘학습’을 통해 가설의 적절한 매개변수 값들을 찾아나가게 됩니다. 그러기 위해서는 가설로 예상한 값과 실제 값의 차이를 계산하는 비용함수 (Cost Function)이 필요합니다. 비용함수는 손실 (Loss)라고 부르기도 합니다. 선형 회귀에서는 다음과 같이 비용함수를 정의합니다.
학습의 방향은 다음과 같이 비용함수가 최소화되는 매개변수 W와 b를 찾는 것입니다.
어떻게 비용함수가 최소화되는 매개변수를 찾을 수 있을까요?

Gradient Descent Algorithm

답은 비용함수의 기울기 (gradient)를 구한 다음에 기울기와 반대되는 값으로 매개변수들을 조금씩 움직여가는 방법입니다. 이것을 경사 하강법이라고 합니다. 경사 하강법을 지속적으로 적용하면서 함수 값은 극소점 (local minimum)을 찾아가게 됩니다.

참고: https://en.wikipedia.org/wiki/Gradient_descent 경사 하강법의 특징 중 하나는 함수의 최소값이 아닌 극소값을 찾아가는 것입니다. 볼록 함수 (convex function) 경우에 이러한 문제를 방지할 수 있습니다.

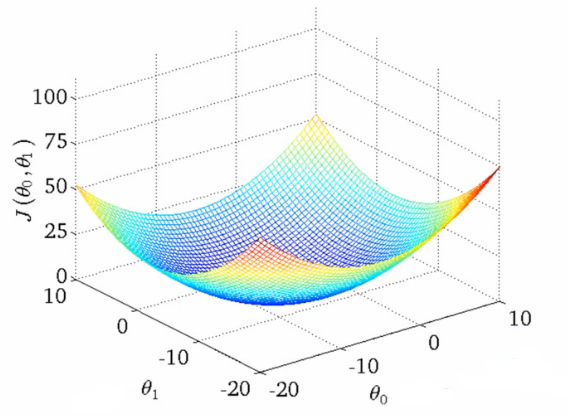
볼록함수

볼록 함수가 아닌 함수 출처: https://www.coursera.org/learn/machine-learning
Multivariate Linear Regression
투입 변수가 여러 개이더라도 방식은 똑같습니다. 다만 변수를 하나로 묶어서 다음과 같이 행렬의 연산으로 나타낼 수 있습니다.
선형 가설 설정 -> 비용 함수 설정 -> 경사 하강법을 통한 극소점 찾기
로지스틱 회귀 (Logistic Regression)
이진 분류 (Binary Classification) 문제는 선형 회귀로는 풀리지 않습니다. 이진 분류 문제는 주어진 투입 값에 대해 산출 값이 0 아니면 1로 나오기 때문에 선형 회귀를 적용하는 것은 적절하지 않습니다. 선형 함수를 사용하게 되면 0에서 1 사이를 넘어가는 값을 갖게됩니다. 따라서 다음와 같은 시그모이드 함수를 사용합니다.

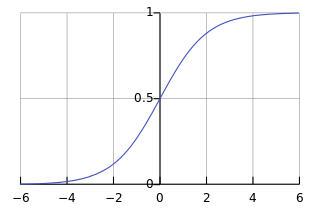
출처: https://en.wikipedia.org/wiki/Sigmoid_function
시그모이드 함수 식은 다음과 같습니다. 이러한 시그모이드 함수를 가설로 사용하는 문제를 로지스틱 회귀라고 합니다. 가설에 대한 식은 다음과 같습니다.
비용함수 또한 달라집니다. 아까 선형 회귀의 비용함수와 똑같이 비용함수를 잡으면 함수가 볼록하지 않습니다.

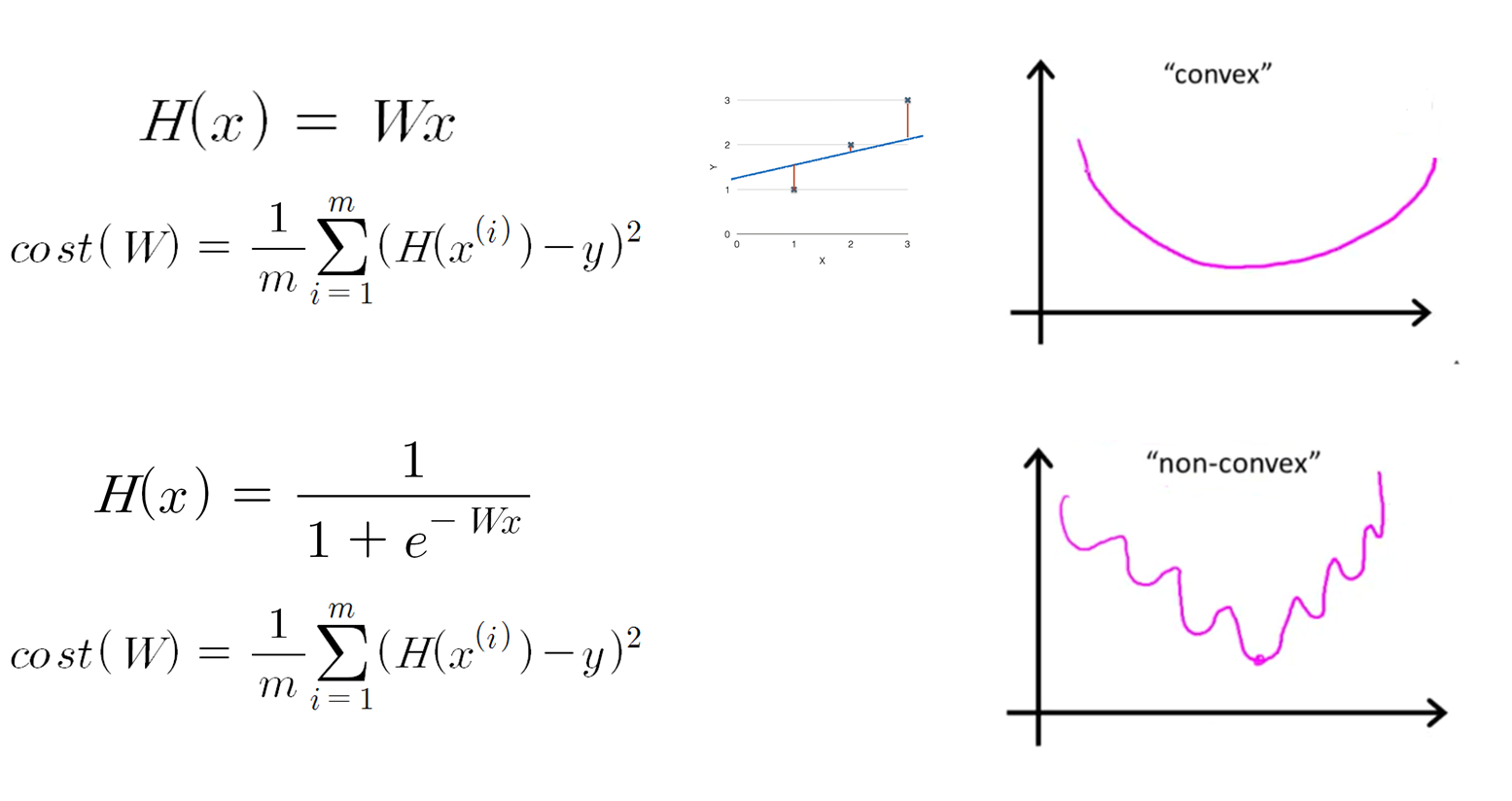
출처: https://hunkim.github.io/ml/ 그래서 로지스틱 회귀의 경우에 비용함수는 아래와 같이 표현합니다.

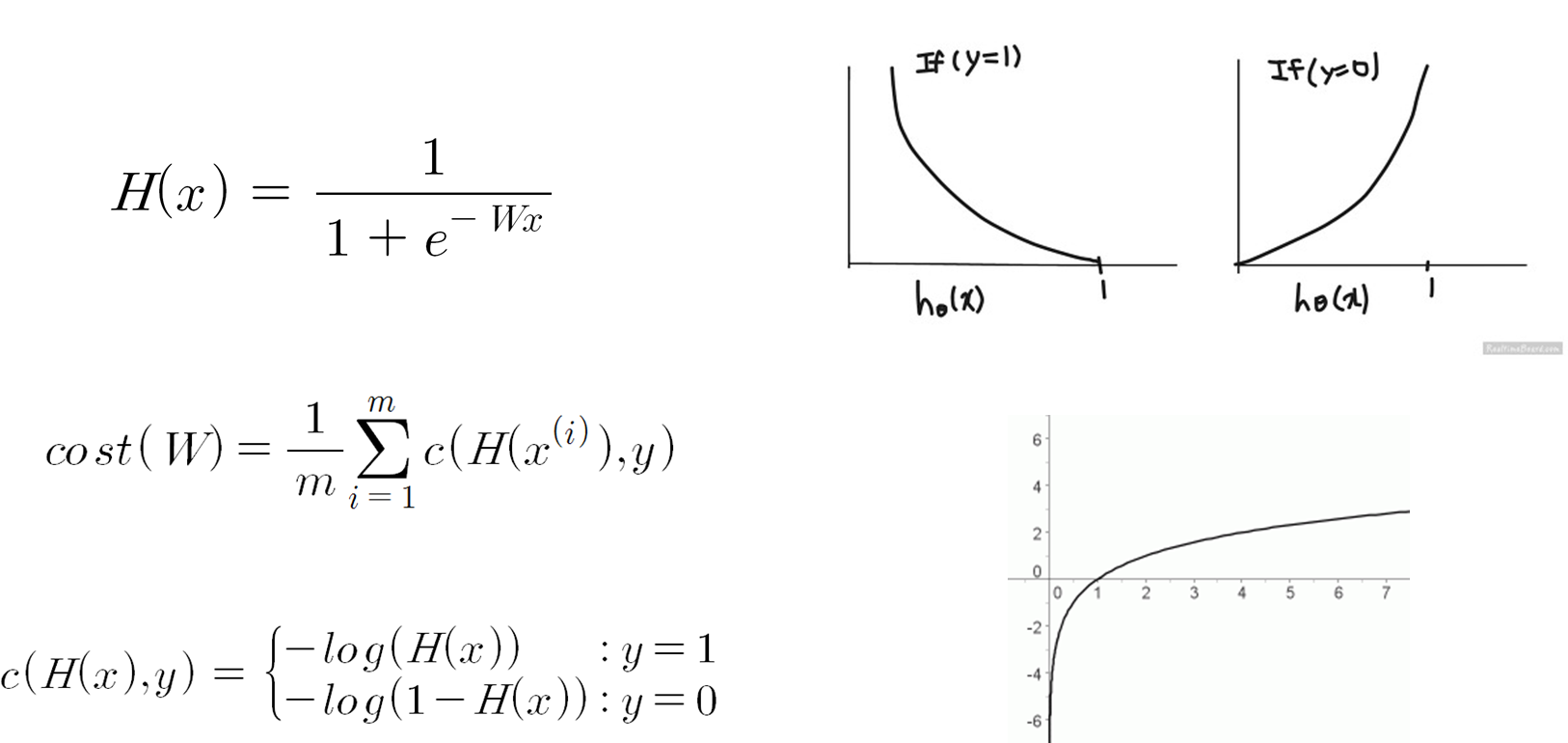
출처: https://hunkim.github.io/ml/ 그 뒤로는 똑같이 경사 하강법을 적용하여 극소값을 찾아가게 됩니다.
Softmax Regression
다중 (multiclass) 혹은 다항 분류 (multinomial classification) 경우에는 로지스틱 회귀와는 조금 다른 함수를 사용하게 됩니다. 기본적인 아이디어는 N개의 분류가 있을 때, N개의 이진 분류기를 사용하는 것입니다. 다음과 같이 하나의 행렬로 나타낼 수 있을 것입니다.

출처: https://hunkim.github.io/ml/ 계산된 y 값들은 모두 실수 범위의 값을 갖습니다. 여기서 소프트맥스 (softmax)라는 특별한 함수를 사용하여 y 값들을 모두 확률로 변환시켜줄 수 있습니다. 이런 방식의 회귀를 소프트맥스 함수의 이름을 따서 소프트맥스 회귀라고 부릅니다.

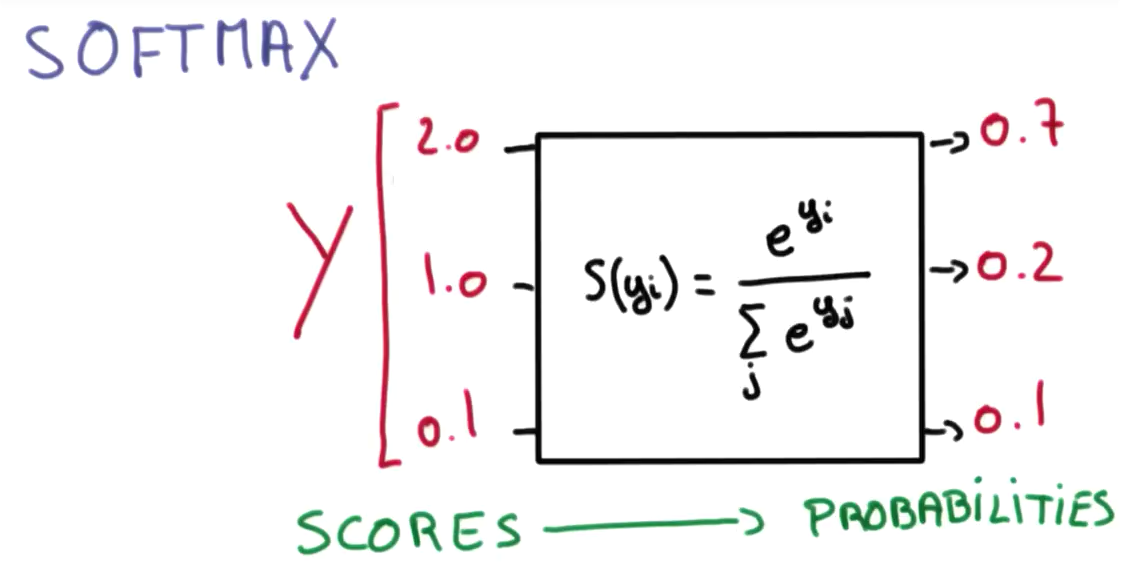
출처: https://hunkim.github.io/ml/ 소프트맥스 함수는 다음과 같습니다.
비용함수 또한 로지스틱 회귀와는 다른 형태를 가지고 있습니다. 비용함수는 다음과 같습니다.
크로스-엔트로피 (cross-entropy) 함수라고 합니다. 여기서 \( \hat{y_i} \)는 실제 산출 값, \( y_i \)는 예측 값을 의미합니다. 실제 산출 값은 원핫 인코딩 (one-hot encoding) 방식을 통해 분류에 해당하는 값만 1로 나타내어 집니다. 밑의 그림은 비용함수를 좀 더 시각적으로 나타낸 것입니다.

출처: https://hunkim.github.io/ml/